机器学习可应用在各个方面,本篇将在系统性进入机器学习方向前,初步认识机器学习,利用线性回归预测波士顿房价;
原理简介
利用线性回归最简单的形式预测房价,只需要把它当做是一次线性函数y=kx+b即可。我要做的就是利用已有数据,去学习得到这条直线,有了这条直线,则对于某个特征x(比如住宅平均房间数)的任意取值,都可以找到直线上对应的房价y,也就是模型的预测值。
从上面的问题看出,这应该是一个有监督学习中的回归问题,待学习的参数为实数k和实数b(因为就只有一个特征x),从样本集合sample中取出一对数据(xi,yi),xi代入kx+b得到输出y^i,MSE可以衡量预测输出与样本标注的接近程度,所以把MSE作为这个问题的损失函数,对于共m mm个样本的集合,损失函数计算为:J(k,b)=1i=1∑m(yi−yi)2
一般需要遍历数据集迭代多次,才能得到一个较好的结果
波士顿房价数据集
房价预测的实现将基于sklearn(scikit-learn),sklearn中有多种数据集:
-
自带的小数据集(packaged dataset):sklearn.datasets.load_<name>
-
可在线下载的数据集(Downloaded Dataset):sklearn.datasets.fetch_<name>
-
自定义生成的数据集(Generated Dataset):sklearn.datasets.make_<name>
首先从sklearn的数据集获取内置数据集中的即波士顿房价数据:
from sklearn.datasets import load_boston
|
导入其他功能包和模块,导入线性回归模型:
# 使用sklearn 中的 train_test_split 划分数据集
from sklearn.model_selection import train_test_split
# 使用 sklearn 中的线性回归模型进行预测
from sklearn.linear_model import LinearRegression
# 使用 matplotlib 中的 pyplot 进行可视化
import matplotlib.pyplot as plt
|
加载数据集:
# 加载波士顿房价数据集,返回特征X和标签y
X, y = load_boston(return_X_y=True)
X.shape # (506, 13)
y.shape # (506,)
|
取出一个特征作为x:
# 只取第6列特征(方便可视化):住宅平均房间数
# 注意切片区间左闭右开
X = X[:,5:6]
|
划分为训练集和测试集,测试集取20%:
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2, random_state=2020)
|
使用到sklearn.model_selection.train_test_split,函数形式为:
train_test_split(train_data, train_target, test_size, random_state,shuffle)
|
-
test_size:浮点数,在0 ~ 1之间,表示测试样本占比
-
random_state:随机种子,种子不同,每次调用时采样的样本不同;种子相同,每次调用时采样一致
-
shuffle = True,打乱样本数据的顺序
严格来说,对于有监督学习的数据集应分为训练集,验证集,测试集;训练集和验证集有标注,测试集没有标注,泛化能力在验证集上进行检验
划分后的训练数据:
X_train.shape # (404, 1)
y_train.shape # (404,)
|
建立线性回归模型
在sklearn下,机器学习建模非常方便:
-
实例化模型,输入合适的超参数会使模型性能提升
-
输入数据训练
-
验证模型
建立线性回归模型如下:
# 创建线性回归对象
regr = LinearRegression()
# 使用训练集训练模型
regr.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = regr.predict(X_test)
|
注意到模型直到接收到训练数据,才最终确定具体形式,比如发现输入数据是(404,1),才确定线性回归形式为kx+b,而不是kx+cx+b
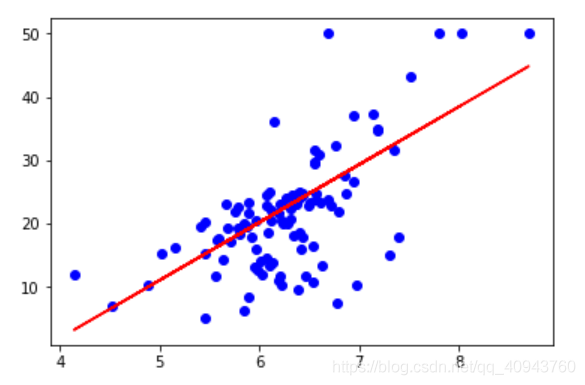
# 画测试数据散点图
plt.scatter(X_test, y_test, color='blue')
# 画线性回归模型对测试数据的拟合曲线
plt.plot(X_test, y_pred, color='red')
# 显示绘图结果
plt.show()
|
打印模型参数有(注意区分参数和超参数):
# 打印斜率和截距
print('斜率:{}, 截距:{}'.format(regr.coef_,regr.intercept_))
|
结果为:
斜率:[9.11163398], 截距:-34.47557789280662
|