1. 引言
本文是数独游戏问题求解的第二篇,在前文中我们使用回溯算法实现了最简单版本的数独游戏求解方案。本文主要在前文解决方案的基础上,来思考如何通过改进来提升数独问题求解算法的性能。
闲话少说,我们直接开始吧。 :)
2. 前文回顾
我们首先来回顾下前文的回溯算法,如下图示:
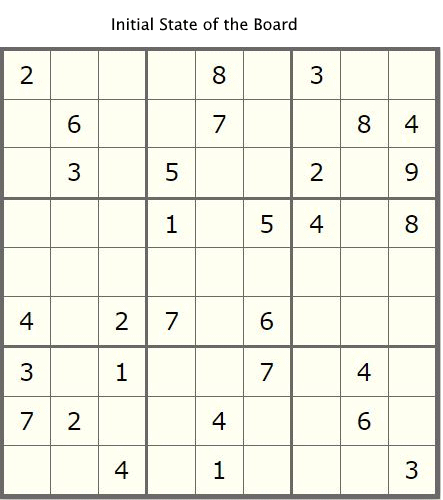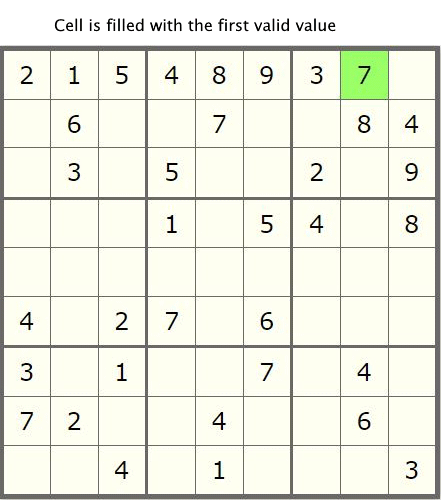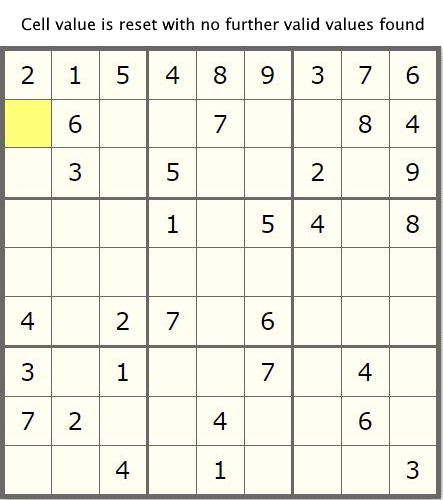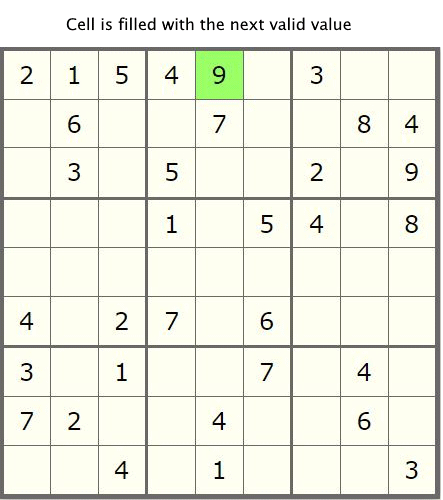
在前文中,我们引入了回溯算法来对数独问题求解,通过迭代每个子单元格cell的所有可能取值来暴力解决该问题,直到引入数独九宫格中的新值与属于同一行,列或block块的子单元格中确定值之间没有冲突为止。这种解决方案虽然可以有效解决该问题,但是它绝对不是最佳的解决方案,因为它没有合理利用数独九宫格中提供的附加先验信息。下面,我们来一步步对前文算法进行优化吧。。。
3. 减少非比要的迭代次数
优化上述算法的第一个想法来自于这样的观察,我们的算法按顺序迭代所有数字1到9,直到它找到一个与已经包含相同值的同一行,列或block块中的另一个单元格不冲突的值。但是,数独九宫格中一些确定值会已经为我们提供了一些信息,说明哪些数字不可能添加到某个子单元格cell中。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# Solve Sudoku using backtracking
def solve(board):
blank = findEmpty(board)
if not blank:
return True
else:
row, col = blank
for i in range(1,10):
if isValid(board, i, blank):
board[row][col] = i
if solve(board):
return True
board[row][col] = 0
return False
|
我们优化的思路是首先扫描我们的数独九宫格,将每个子单元格的所有可能的合法候选值保存在内存中然后再逐个迭代它们,而不是迭代所有数字。参考下图,演示了数独九宫格的 2 个子单元格的候选值的集合。正如我们的游戏规则所暗示的那样,每行,每列和每个block块不能包含相同的数字,因此在属于给定子单元格的同一行,列和所属block块的单元格中已经确定的所有数字都被排除在外。
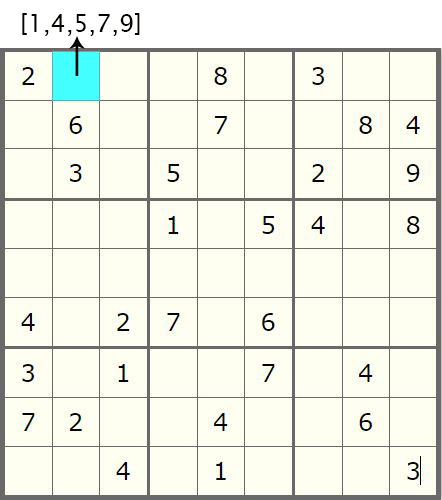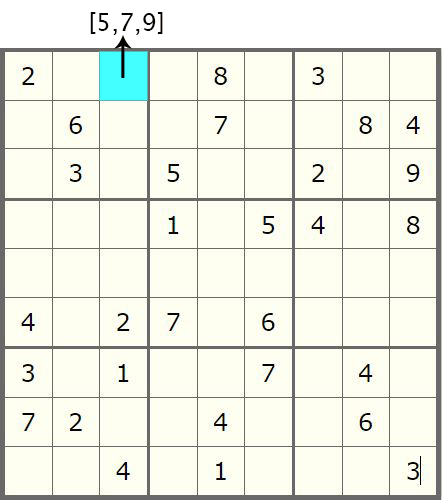
既然有了优化思路,那么我们接下来就可以来用代码实现上述想法啦.
3.1 生成候选值字典
接着我们需要一个数据结构(这里我们选用字典)来保存每个子单元格的候选值列表,该函数通过遍历整个九宫格中空的子单元格并调用我们的allowedValues()函数来返回子单元格的候选值列表.
样例代码如下:
|
1
2
3
4
5
6
7
8
9
|
# Store in a dictionary the legitimate
# values for each individual cell
def cacheValidValues(board):
cache = dict()
for i in range(9):
for j in range(9):
if board[i][j] == 0:
cache[(i,j)] = allowedValues(board,i,j)
return cache
|
3.2 生成候选值列表
在上小节中的allowValues() 函数与我们在前篇文中看到的isValid() 函数具有类似的逻辑,但在本例中,它返回值为每个子单元格所提取到的合法数字的列表。
样例代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
def allowedValues(board,row,col):
numbersList = list()
for number in range(1,10):
found = False
# Check if all row elements include this number
for j in range(9):
if board[row][j] == number:
found = True
break
# Check if all column elements include this number
if found == True:
continue
else:
for i in range(9):
if board[i][col] == number:
found = True
break
# Check if the number is already included in the block
if found == True:
continue
else:
rowBlockStart = 3* (row // 3)
colBlockStart = 3* (col // 3)
rowBlockEnd = rowBlockStart + 3
colBlockEnd = colBlockStart + 3
for i in range(rowBlockStart, rowBlockEnd):
for j in range(colBlockStart, colBlockEnd):
if board[i][j] == number:
found = True
break
if found == False:
numbersList.append(number)
return numbersList
|
3.3 函数调用
有了我们的单元格候选值缓存字典,下面我们准备测试该方案是否会显着提高我们的程序性能。
为此我们还需要将 solve() 函数替换为一个新的函数solveWithCache(),该函数只迭代每个子单元格cell的合法值列表,而不是所有数字 1–9。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
def solveWithCache(board, cache):
blank = findEmpty(board)
if not blank:
return True
else:
row, col = blank
for value in cache[(row,col)]:
if isValid(board, value, blank):
board[row][col] = value
if solveWithCache(board, cache):
return True
board[row][col] = 0
return False
|
在实现所有改动后测试我们的代码为我们提供了所需的结果,与我们的第一个版本相比,跑同样50组测试用例执行时间明显缩短:
|
1
|
The execution time of above program is : 15.41820478439331 s
|
4. 总结
本文为数独游戏求解的第二篇,主要基于第一篇的回溯思想来思考如何利用数独九宫格的先验思想来减少回溯的迭代次数,进而提升算法提升效率,并给出了完整代码实现.
|